How word frequency affects language models
As I started my PhD a few months ago, I believed that contextual embeddings coming from pre-trained language models aimed at representing words in a vector space as humans might in their thought process. In other words, I thought the BERT-like embedding spaces tended to learn the underlying metric of word relatedness depending on context.
To the impish, this belief is easy to catch because of the great adaptability of these embeddings during fine-tuning or domain adaptation. This adaptability leads to think that the embedding space captures most of the semantic and syntactic substance of the words, which only needs to be extracted and slightly adjusted for downstream tasks.
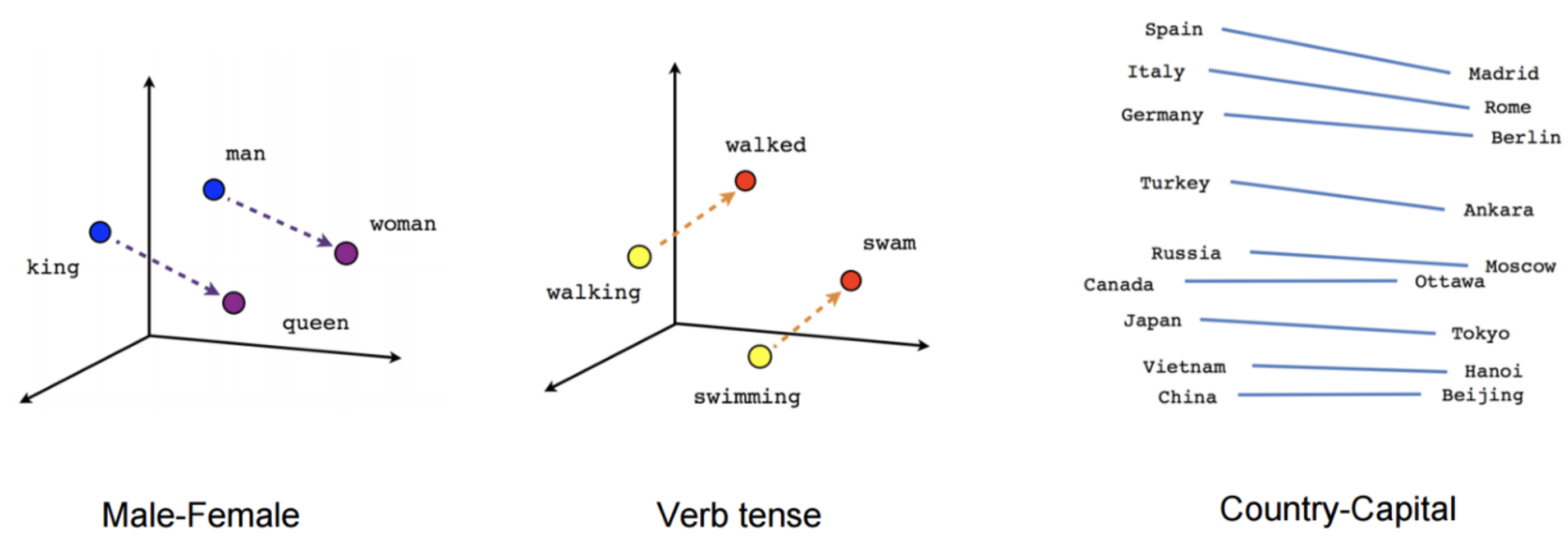 (Arguable) beliefs about Word2Vec models that may have impacted my understanding of contextual representations. These embeddings were isotropic in the sense that most of the representations were close to orthogonal to each other, which makes sense in a high-dimension space. (source: OpenClassrooms)
(Arguable) beliefs about Word2Vec models that may have impacted my understanding of contextual representations. These embeddings were isotropic in the sense that most of the representations were close to orthogonal to each other, which makes sense in a high-dimension space. (source: OpenClassrooms)
A probability distribution on a vector space is said to be isotropic if we expect a similar density when considering every direction of the space. The covariance matrix of a perfectly isotropic distribution is the identity $I_D$.
That’s with this belief in mind that I started reading about the representation degeneration problem.
Representation degeneration of language models
To be honest, I already knew that LM representations were far from perfect in the sense I describe above. When working on downstream tasks for industrial applications, or when trying to use naive zero-shot sentence embeddings, one can clearly see inherent flaws, for instance when it comes to comparing metrics like cosine similarity with our human perception of similarity. This raises concerns about the architectures we use, the data we pre-train with, the optimization parameters we take into account, the scale of our models, among other things.
But one factor that was (is?) often under-estimated is the learning objective itself, i.e. the loss. Until you read the excellent paper Representation Degeneration Problem in Training Natural Language Generation Models (Gao et al., ICLR 2019).
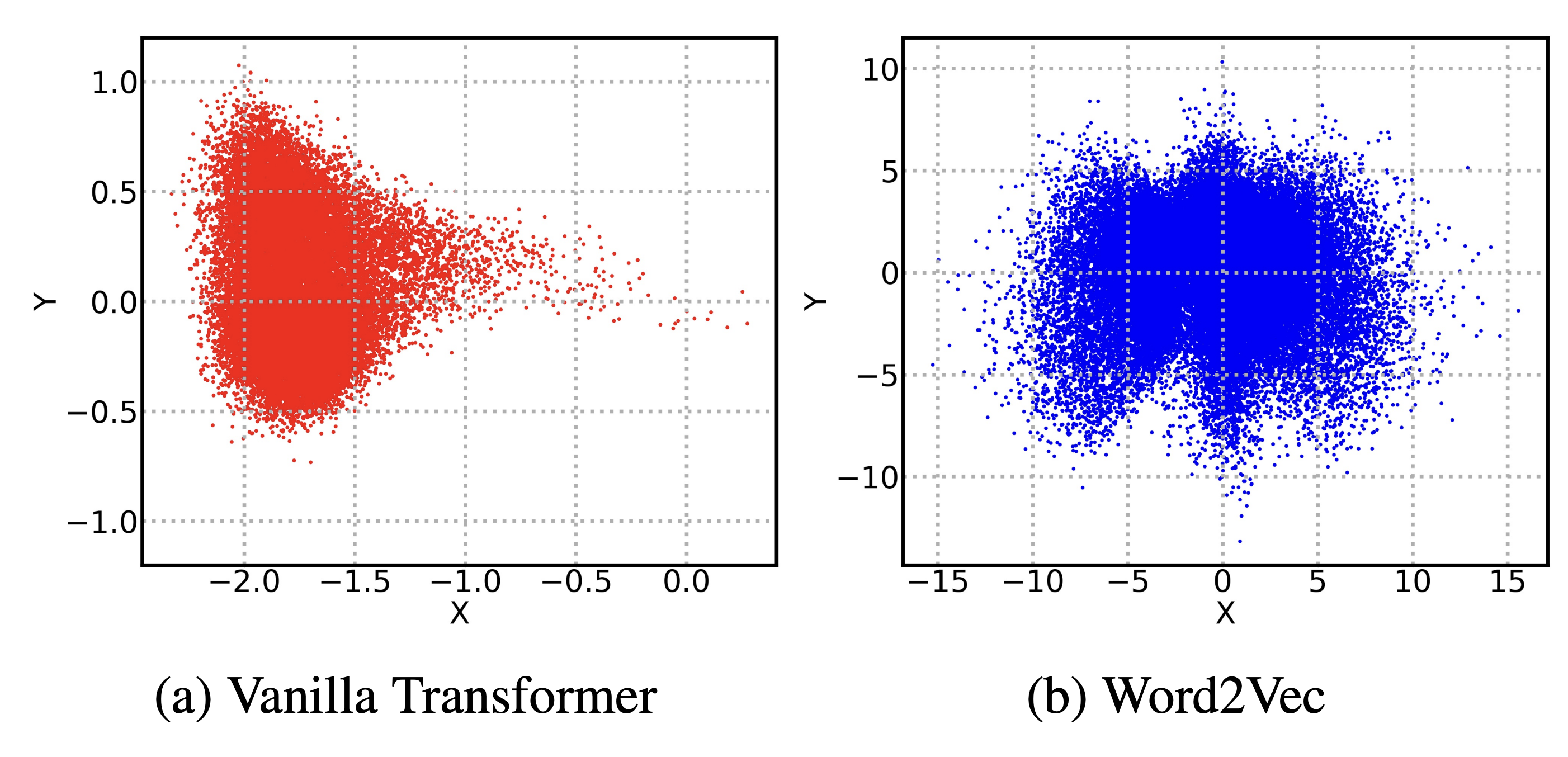 The cone problem: if you scatter the first singular dimensions of contextual representations, a cone appears.
The cone problem: if you scatter the first singular dimensions of contextual representations, a cone appears.
This paper argues that cross-entropy loss inherently pushes low-frequency categories (e.g. tokens) away from the origin in a given direction. Let’s dive into this.
The problem with cross-entropy and rare words
The uniformly negative direction
The cross-entropy loss is used to learn how to predict tokens in many language models. It goes like this:
\[\mathcal{L}_{ce} = \frac{1}{N} \sum_{k=1}^N - \log(\frac{\exp(\langle h_k,w_k \rangle)}{\sum_{l=1}^{V}\exp(\langle h_k,w_l \rangle)})\]where $h_k$ describe the hidden states for the $N$ tokens used for training, and $w_l$ are the vectors from the last projection layer mapping to the vocabulary prediction in $\mathbb{R}^V$.

Now let’s focus on the extreme case of word $S$ (for sad) that never appears in the training set but is included in the vocabulary. If we freeze all parameters except for $w_S$, the optimization problem becomes:
\[\min_{w_S}{\frac{1}{N} \sum_{k=1}^N -\log\frac{C_1}{\sum_{l\neq S}\exp(\langle h_k,w_l \rangle) + \exp(\langle h_k,w_S \rangle)}} = \min_{w_S}{\frac{1}{N} \sum_{k=1}^N \log(\exp(\langle h_k,w_S \rangle) + C_2)}\]where $C_1$ and $C_2$ are constant with respect to $w_S$.
Let’s imagine that the model is on the edge of converging, and that the structure of the hidden states $h_k$ doesn’t evolve much with new samples. What Gao et al. show is that there will most likely exist a specific direction $v$ so that $\exp(\langle h_k,v \rangle)$ is negative for all $k$. In other words, for a fixed structure of the hidden states, there will almost surely exist a direction for the $w_S$ that will minimize the loss.
This uniformly negative direction thus emerges as an optimal direction for the loss function when optimizing $w_S$, possibly pushing it towards infinite magnitude to amplify the effect. This means that even after the hidden states have converged, the input embeddings of unused words are still endlessly pushed in a specific direction.
Rare words
Gao et al. show that this phenomenon smoothly decays as word frequency increases, meaning it also happens for rare words. The thing is, natural language is full of rare words. Here is a plot of the distribution of BERT tokens in the Wikitext-103 dataset:
As we see, a vast majority of words can be described as relatively rare, and may be affected by the smooth version of the uniformly negative direction issue.
Gao et al. actually provide a bound on the effect of frequency on the smoothness of the uniformly negative direction issue, which could give an idea of what range of token frequency is affected depending on the structure of the contextual embedding mapping.
This is probably not the only explanation for representation degeneration and its link to token frequency, but it hints that there may exist some
As a result, if one takes a look at the representations in BERT-base for instance, it appears that frequency plays a huge part in the representation degeneration effect: 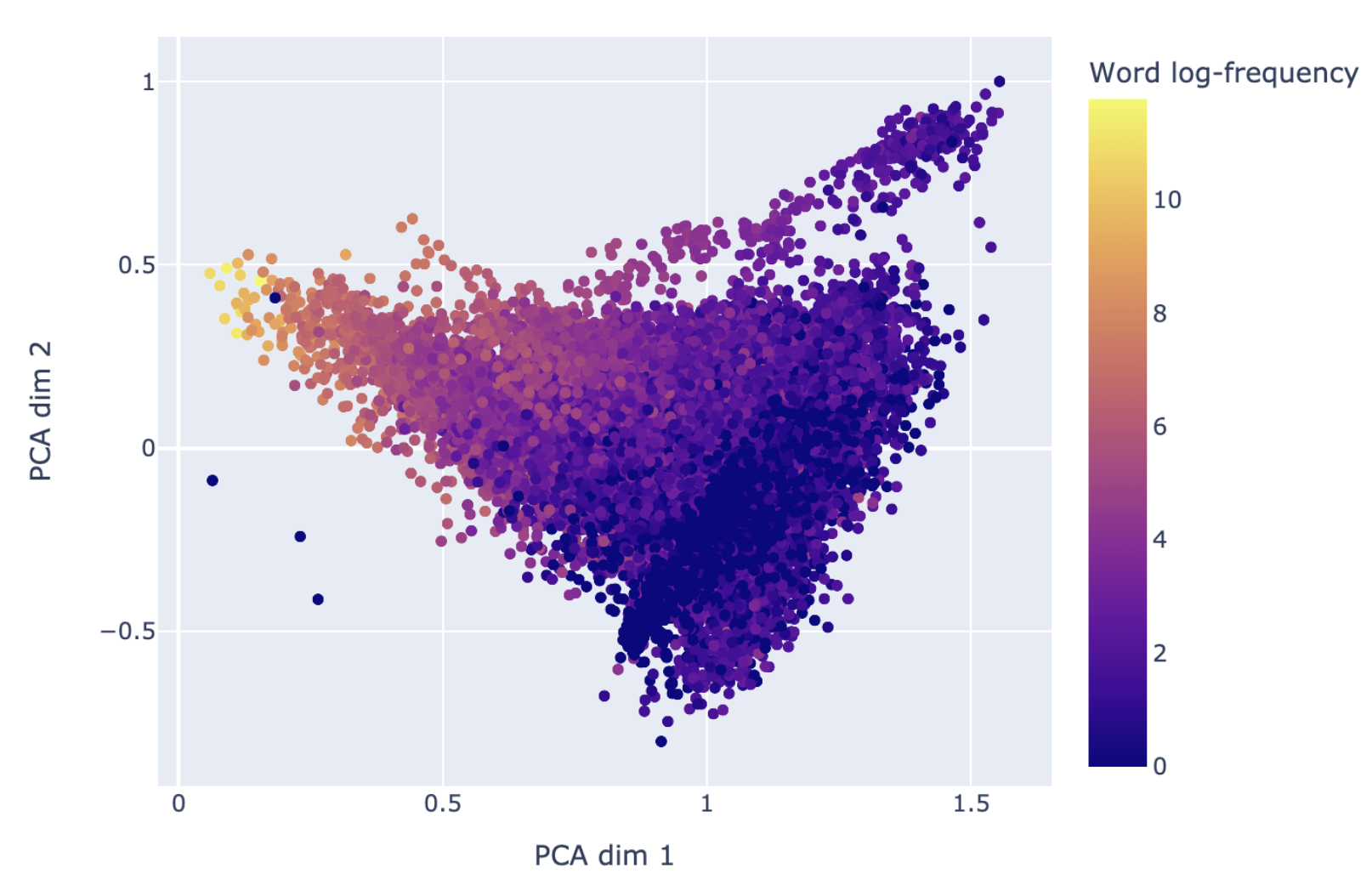 The “cone” of BERT’s input representations with respect to frequency
The “cone” of BERT’s input representations with respect to frequency
Why does it matter?
When I first talked about the “cone” around me, I often got the following reactions:
Okay so the first two singular dimensions of the embeddings are skewed, but we still have 754 left, we should be fine, right?
Yes, but not really. For instance, if you take a look at the representations of any given layer of a BERT model, you’ll find that their singular value distributions are very spiked. Here we focus on the input layer for the sake of simplicity:
If you take a look at the explained variance ratio on the graph above, you see that the first components explain a big part of the variance. If these are skewed, then a significant part of the “information” contained in the embeddings is impacted.
Is it really bad? I mean we get good performance on downstream tasks so why bother?
There are two main arguments in favor of looking for isotropy in contextualized representations:
- It has proven efficient in the case of sentence encoder embeddings. SimCSE, BERT-flow and BERT-whitening are all based on making sentence representations more isotropic.
- To the best of my knowledge, isotropy has not been achieved (without post-processing) yet. The models that end up being more isotropic (e.g. ELECTRA as we’ll see below) show better performance and cheaper training.
Degeneration and cosine-similarity
Cosine-similarity is a metric ranging from -1 to 1 that reflects angular proximity between vectors. Looking at the histogram of average cosine-similarity between two random representations from the last layer of BERT shows that the embedding space covers a small portion of the possible directions. Not only the average cosine-similarity is almost 0.4, but there also is almost no pairs with a negative similarity, which is a sign of poor “angular diversity”:
Perfectly anisotropic representations would be orthogonal to one another in average, which would induce a smooth distribution of cosine similarities centered around 0.
This phenomenon occurs for a lot of models, and for almost every depth, as shown in Bihani et al.: 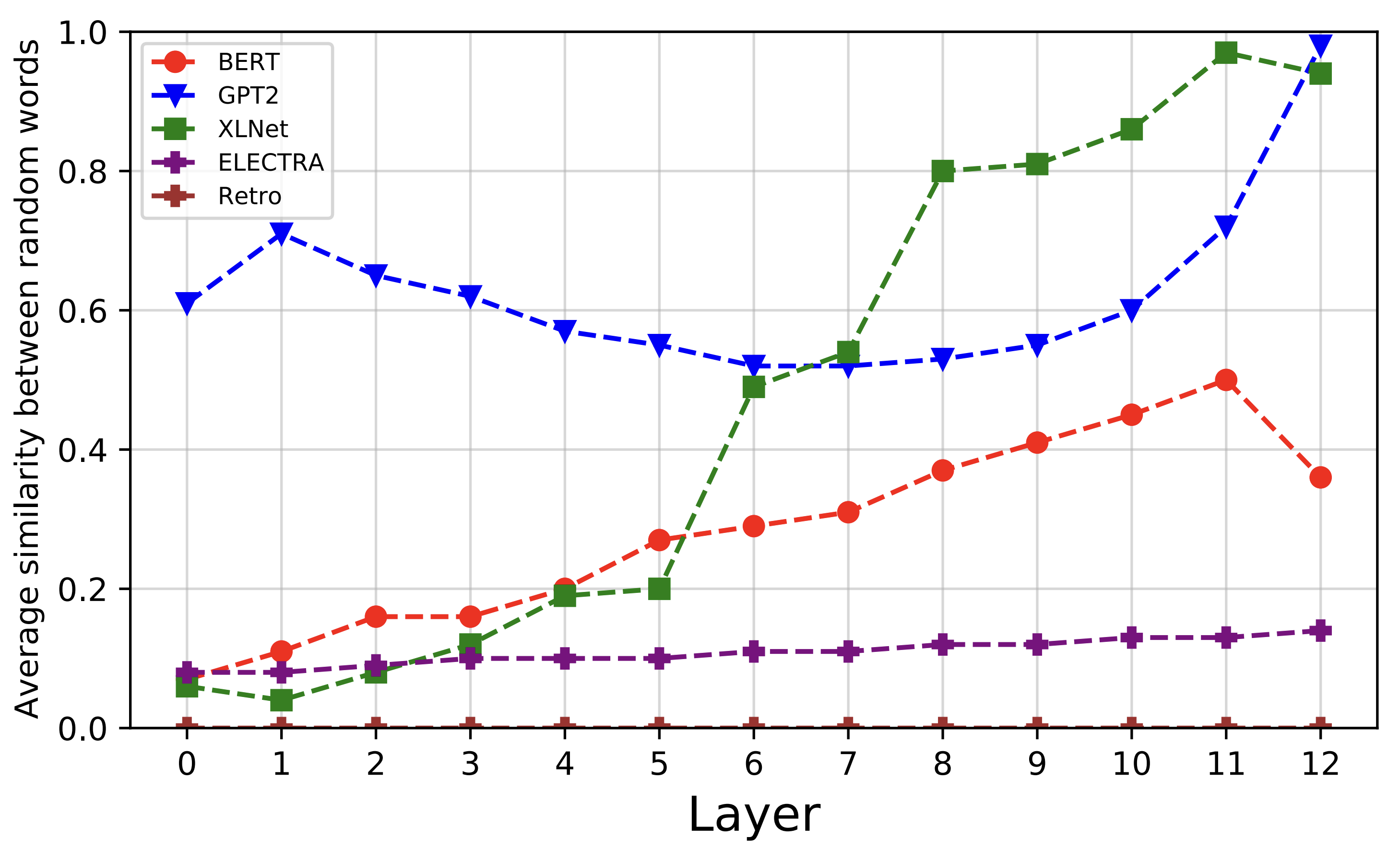 Average cosine similarity for representations at different depths in several models. Notice how Electra’s values show more isotropy and are constant along the layers. Electra is the only model that isn’t trained using cross-entropy in the vocabulary space.
Average cosine similarity for representations at different depths in several models. Notice how Electra’s values show more isotropy and are constant along the layers. Electra is the only model that isn’t trained using cross-entropy in the vocabulary space.
It appears that the closer to the vocabulary prediction we take the representations from, the less isotropic they are. Notice how the last layers of generative models (GPT-2 and XL-NET) display a very poor angular diversity as the embeddings are almost perfectly aligned in average.
As Bihani et al. show in their paper Low Anisotropy Sense Retrofitting (LASeR) : Towards Isotropic and Sense Enriched Representations, removing the first few singular dimensions can drastically reduce anisotropy as measured by cosine-similarity.
As I reached this point in my understanding of the representation degeneration problem, I gathered that corpus frequency played an important part in the structure of the contextual representations, and that this structure was highly anisotropic. Are there any hints that these two phenomena are linked? Is the highly skewed word frequency of natural language the cause of anisotropy in the context of vocabulary space prediction?
Frequency and the embedding space
We saw visually that there is a strong correlation between word frequency and the embedding space, but can we measure it? A way to answer this question is to compare the singular spectrum and the word frequency associated to each token. For each singular vector, we look at the correlation between the weights associated to the embeddings in this singular component and the word frequencies associated to the embeddings. Let’s look at the absolute value of the Pearson correlation between these two variables with respect to the singular value:
This plot shows that the highest singular values correspond to components that are correlated with frequency (up to 25%). Once again, as we see here, the singular spectrum of the embeddings is really spiked with singular values decaying pretty fast (here at log-scale on the x-axis). This means that most of the variance of the embeddings has some correlation with the corpus frequency. This correlation is significative for these singular values, as the p-value of the Pearson test shows:
My current research focuses exactly around the hypothesis presented in this post:
Hypothesis : Using vanilla cross-entropy loss to train language models results in strong anisotropy because of the shape of the Zipf’s law.
Takeaways
Summary
- The representations of most language models lie in a cone in the embedding space
- This might be explained by how cross-entropy behaves with rare words (Gao et al.)
- Removing the strongest singular components makes the representations more isotropic (Bihani et al.)
- The strongest singular components are correlated with word frequency
Open questions
- Is smoothing the effect of frequency on the representations during pre-training reducing the induced anisotropy in the representation space?
- Is a language model with more token-level anisotropy better at downstream tasks?
- Can regularizing approaches such as contrastive losses improve isotropy during pre-training? Would the resulting embeddings be less correlated with frequency?
References
SimCSE: Simple Contrastive Learning of Sentence Embeddings (Gao et al., 2022)
On the Sentence Embeddings from Pre-trained Language Models (Li et al., 2020)
Whitening Sentence Representations for Better Semantics and Faster Retrieval (Su et al., 2021)
Thanks to Roman Castagné and Rian Touchent for their comprehensive feedback, and to Benoît Sagot and Eric Villemonte de la Clergie for their supervision!
This work was funded by the PRAIRIE institute as part of a PhD contract at Inria Paris and Sorbonne Université.